Learn interpreting audio measurements with Cavern

About impulse responses

The impulse response is a major element of advanced audio measurements, and like the excitement response, it contains everything about the room. The impulse response (IR for short) is simply the excitement response divided by the excitement signal, which means it's the difference between the two. As such, it's the raw description of the system, just the way it affects the sound and nothing else. As the name suggests, if there's an impulse response, there must be an impulse signal. There is, and it's called Dirac-delta. It would be the measurement if it was a single point in time, every single frequency at the smallest unit an audio system can handle: a single sample. What a sample is, is described in the Info page about Codecs. While we could technically use a Dirac-delta as a measurement signal, and it would make the measurements instantaneously fast, there is a reason we don't use it. The longer we measure, the more precise the measurement gets, because there is so much noise for so many frequencies in that little point in time that the recording would be unusable. So we use swept sine waves, which lay out the frequencies on a very long time scale compared to a Dirac-delta.

The impulse has the sound of a clap or a film slate, and the recording of it will be a clap distorted by the speakers' or the room's effect. This means if there is a delay, the impulse will be delayed by that amount too. Also if there are echoes, we could see multiple small impulses with their exact additional delay and their exact gain difference. These are the markers we're looking for when searching for acoustic issues.

Finding echoes with impulse responses

Because each echo should result in an impulse spike, we just need to find how much time they appear after the initial sound wave to be able to work with them. First, we need to show the impulse responses, which is a Complex QuickEQ feature, found on the IR-filter tab, with the Show impulse responses toggle. They can be scaled for evaluation with the Right IR window slider after its toggle is enabled. Here's an IR of an untreated small room:

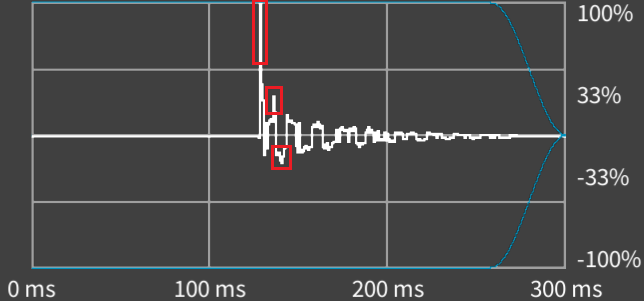
We can use the Right IR window slider to align its most important points to gridlines as it cuts off the right side of the impulse. With this method we know that

the initial impulse is at 130 ms,
the first major echo is at 136 ms,
the second major echo is at 141 ms,
and when the curve becomes a blob without distinct rising or falling sections, so anything to the right from the second echo, are just reverb.

It's not a problem that the initial impulse took 130 ms to go through the entire system. Most of it is the internal latency of Cavern's microphone handling and is properly removed when QuickEQ exports delays. We only need the differences, so subtract the initial impulse from the offsets of major echoes, and divide them by 1000 to get the time in seconds:

first major echo: 136 ms - 130 ms = 6 ms = 0.006 seconds,
second major echo: 141 ms - 130 ms = 11 ms = 0.011 seconds.

The second step is to calculate how much sound waves travel in that time. Cavern uses 347 meters per second as the speed of sound, which is calculated in a 25.4 °C room with air conditioning on, let's multiply our results with that:

first major echo: 0.006 s * 347 m/s = 2.08 m = 208 centimeters,
second major echo: 0.011 s * 347 m/s = 3.82 m = 382 centimeters.

This is how much longer path the echoes took to get to the microphone, we just need to find out where it could have bounced off to result in that extra distance. There is a disturbingly analog, but genius method, without any fancy software to perfectly find a reflection point knowing this extra distance. Take how far away the measured channel is from the microphone, let's say it's 4 meters in this example, so 400 centimeters. Add the echo's extra distance to that, for the first one, it's 400 + 208 = 608 centimeters. Here comes the analog part: take a rope, wind down exactly the combined distance from it, 608 cm in this case, and put a knot on the microphone from that point. Don't cut the rope, it's just wasting a perfectly good rope, you can put a knot on the mic without that. For the loose end, attach it to the speaker somehow, for example, to its top, and putting your phone on it to keep it in place. Now comes the part to determine where to put the acoustic panels: try placing the rope on any surface directly left, right, up, or down from the direct path of the sound, and when it's holding there perfectly straight, you've found the exact location that caused that reflection. Try putting acoustic panels at that location to mitigate the echo. Do the same with the other major echoes.

Types of calibration systems

The way calibrators work is, they find how much the measured frequency response differs from the target curve, and for example, if sounds on one frequency need to be louder, they just play that specific frequency and its surroundings louder. The precision depends on what system you export to and how they work exactly. There are two main methods for applying a calibration. One is called finite impulse response or FIR for short, the other is infinite impulse response or IIR. Each of them have their pros and cons, but Cavern QuickEQ supports both.

This is only an advertisement and keeps Cavern free.

Infinite impulse response filters

These are the legacy filters, where the ones used for corrections are called peaking equalizers. While IIRs have many shapes and sizes, we're only interested in these, called PEQs for short. They're called peaking because of their bell shape with a distinct peak, they modify the frequency response by adding or subtracting this bell. The width (bandwidth) and height (gain or amplitude) of this bell can be configured. The bandwidth is determined by the Q-factor, the larger it is, the thinner the bell.

Infinite impulse response simply means if we were to measure their impulse responses (filters, just like any audio systems, have responses, as they modify incoming sound), we would have to record it infinitely, because it will still have some sound, even if it's practically silence and way below the noise floor. However, they are mathematically just fancy smoothings applied on the audio signal, so we can define them as a very simple mathematical operation. Because of this, they can have no delay and be performed in perfectly real time. Analog filters are always IIR. However, this smoothing has a side effect: it breaks the time balance between sounds lower than the filter's frequency, and the ones higher than it, that's why we say IIRs "break the phase". If we use a lot of them, these very small imbalances start to add up, making the corrected channel unalignable with the others, so we limit their number to around 15.

Let's recap: IIRs are very easy to compute, PEQs are very easy to set up because they only have 3 properties, and they can be used for correction with no delay added to the sound, but they break the phase balance. This is the main issue why they got replaced in all modern correction software, but the issues don't end here. IIRs are just not that precise. You've seen how sawtooth-like a frequency response is, there is no way 15 bells can correct it to any reasonable smoothness. Divergences of about +/-3 dB usually remain, and they are very audible. The final issue for calibration systems not recommending IIRs is the speed at which they can calculate them. Unlike FIRs, which will basically be arbitrarily drawn curves, each filter for an IIR correction set has to be tried at every single point, with every single Q-factor, and every single gain. This would be very hard on any computer, so we just test every 10 Hz, every 0.5 dB, etc., we use very painful limitations. One upside for giving only IIR controls to the user is they can easily be entered manually.

Finite impulse response filters

FIRs are generally the "digital" filters: they are filters with a fixed number of data points, their impulse response is described at very small time intervals or samples one after the other. Their length in samples are usually factors of 2 (like 32768 or 65536) for performance reasons. If they can be cut in half, then half again, then half again, computers can process them very fast. This length is their first downside: it determines their resolution. Because an impulse response's length is exactly the number of different frequency bands it can affect, we can calculate a FIR filter's resolution by dividing the system sample rate with the length or size of the filter. Most home theater systems use 48000 Hz as a sample rate, and let's work with QuickEQ's default filter length of 65536 samples: their ratio is 0.7. This means the audio can be corrected at every 0.7 Hz, no matter by how much, no matter how precise. This is overkill, so filter lengths are generally smaller, but QuickEQ is using this resolution to its full potential: for low frequencies, this precision is absolutely needed, and for high frequencies, the correction points are spaced further away. At maximum resolution, QuickEQ has 512 correction points logarithmically spaced, resulting in an astonishing and transparent 1/50th of an octave resolution. This performance is easily available on a PC, but on smaller processors like a MiniDSP 2x4 HD, there are only 1024 data points, and it's using a 96000 Hz sample rate. This means it's resolution is almost 100 Hz. This means there are only 2 correction points for the entire bass range, which makes its FIR mode practically unusable for low frequency corrections.

We've seen that FIRs can be practically infinitely precise, we can draw arbitrary correction curves for any speaker. So what is the downside other than its performance requirement which we mostly have? The only thing is delay. While it is theoretically possible to perform a FIR correction with no delay, that is outside the performance range of even a high-end PC in 2024. We have to process in sample blocks, but not that large sample blocks: most FIR filters process the audio by waiting 256 samples (5 ms on 48 kHz systems), processing it, and then working with the next 256 samples and so on. Other than this, FIRs are perfect for the job: phase distortions are practically nonexistent, only for severe changes like correcting 100 dB in a single band, which we won't do. Some FIRs can have pre-ringing (ringing sound before the actual content is played), and this is accompanied by huge delays. If a FIR has small or no delay, pre-ringing is not possible, because there is no time in the filter for it. QuickEQ is generating these no delay FIR filters by default, but this can be changed if desired. We've seen that FIRs are perfect for the job, and as such, are recommended. The only problem is the support: because they're just a long list of numbers, most manually configurable systems go back to IIRs for convenience, and automatic calibrators use FIR.